This problem is part of a larger rotation problem I made up
to help my friends study physics.
A solid metal wheel with a radius of 3.0 cm and a mass of
2.0 kg is released from rest from the top of a frictionless ramp, 4.0 m from
the ground. It takes 3.0 sec to roll to
the bottom of the ramp without slipping. Determine (a) The wheel’s moment of
inertia, (b) the final linear velocity, (c) the final angular velocity, (d) the
linear acceleration of the wheel, (e) the angular acceleration of the wheel (f)
the number of revolutions the wheel turns through, (g) the net torque on the
wheel, (h) the distance along the ramp that the wheel travels, and (i) the
angle of incline of the ramp in degrees.
A complete walkthrough of the problem can be seen in the
full post.
Problem Walkthrough:
(Note: All calculations are rounded off to the appropriate number of significant figures)
The first thing to do in any physics problem is to make a table of known and unknown values:
The first thing to do in any physics problem is to make a table of known and unknown values:
Note that the initial linear velocity and the initial
angular velocity are both zero, since the wheel starts at rest. In addition,
the radius was converted to meters by dividing by 100.
To solve part a, simply find the appropriate formula for
moment of inertia for the object, plug in the radius and mass, and calculate
the value for I. Since the object is a solid cylinder, the formula becomes:
To solve part b, use the Law of Conservation of Energy to
calculate the linear velocity value. Start with the full equation:
Now the formula must be adapted to fit the context of the
problem. Look at the left side of the equation. The wheel has potential energy
since it starts 4.0 m above the ground.
However, it does not have kinetic energy since it starts at rest.
Additionally, since friction does not affect rolling objects that do not slip
the work from non-conservative forces also cancels out:
On the
right side, notice that there is no potential energy since the wheel is at the
bottom of the ramp. In addition, the final kinetic energy is equal to the sum
of the translational and rotational kinetic energy of the wheel:
Next,
substitute in the proper formula for each form of energy in the new equation:
Although
we have already calculated the rotational inertia of the wheel, substitute the
formula in for I. Notice that the mass cancels out on both sides. In addition,
multiply both sides of the equation by 2 to get rid of the coefficients of ½ to
make further algebraic operations simpler.
Next,
recall the formula for linear velocity that involves angular velocity. Solve
this equation for angular velocity and substitute the resulting expression in for
omega in the energy equation:
Simplify
and solve for the final linear velocity. Then plug in the values from the table
to calculate the value of the final velocity:
For part c, take the formula for final velocity in terms of
angular velocity and solve for the angular velocity. Then plug in the values
for final velocity and the radius of the wheel:
For
part d, use the basic formula for final velocity to solve for the acceleration.
Note that the initial velocity cancels out since it is equal to zero.
For
part e, recall that the angular acceleration is equal to the linear acceleration
divided by the radius.
For
part f, begin with the formula for change of angle. Note that the first term on
the right side cancels out since the initial angular velocity is zero:
The question asks for the answer in revolutions, not radians.
Recall that a full circle has 2 * pi radians in, so divide the radian value by
2 * pi to get the result in revolutions Note that on a calculator, you must put
the 2 * pi in parentheses.
For part g, use Newton’s Second Law in the context of
rotational motion, i.e. net torque equals the moment of inertia times the angular
acceleration:
For
part h, use the normal formula for displacement. Again, initial velocity is
zero so part of the equation cancels out. Additionally, note that this distance
is measured along the incline:
For part g, think of the ramp as a right triangle, and
perform some basic trigonometry to solve for the angle measure using the
inverse sine function:






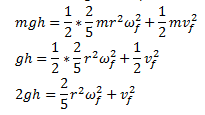










No comments:
Post a Comment